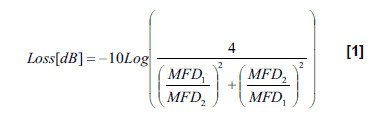
where F2(Θ) is far-field intensity distribution of the test source as a function of the far-field angle Θ for a single dimensional profile1. The Petermann II integral assumes a circularly symmetric waveguide and involves a Hankel transformation of the far-field distribution.
This is a very established method of MFD measurement. Both the National Institute of Standards and Technology (NIST) and its United Kingdom counterpart, the National Physical Laboratory (NPL) use the direct far-field technique to establish MFD standards of optical fiber.
The far-field profile of optical fibers and waveguide sources with an MFD of 10μm or less is quite divergent. For example, for a fiber with a 3 micron MFD, the full width divergence is 40 degrees or larger. Far-field measurements of divergent sources pose a number of unique challenges to be measured accurately in the far-field in order to generate useful MFD results.
In order to measure the far-field distribution of divergent sources, Photon developed a far-field profiling instrument2. This technique was originally developed for laser diodes3,4 and has become the de facto standard for far-field laser diode measurements. It has also proven to be effective and accurate to 0.5% for optical fiber characterization of MFD5. To accommodate the widest range of fibers, Photon designed a far-field profiling system for wave-guides and fibers with more than 60dB of dynamic range of the profile, and a 13.26 cm scanning radius. The large scanning radius minimizes the dependence of the results on sample position, and also reduces bending stress on fibers, which is critical for measurements on polarization maintaining fibers.
This instrument has several distinct advantages over alternative techniques. The first of these is that the light source is measured directly, with no lens, attenuator, or other optics used, which are well known to introduce errors into the measurements.
A second advantage with this tool is that sample positioning has far less influence on the results. Consider the case of a 3-micron MFD. For the near-field measurement, a position accuracy of 1μm was required for an MFD accuracy of ±2%. For a far-field measurement with a 13.26cm scanning radius, ±1% is achieved by a sample position accuracy of ~1mm, more than three orders of magnitude less sensitive. Sample position accuracy of 1mm is easily obtained by simple fixturing, instead of expensive and time consuming positioning equipment.
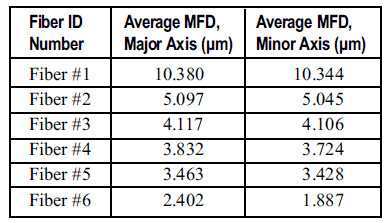
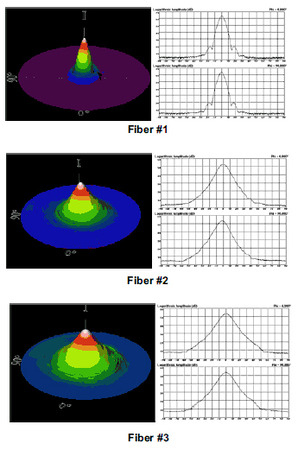
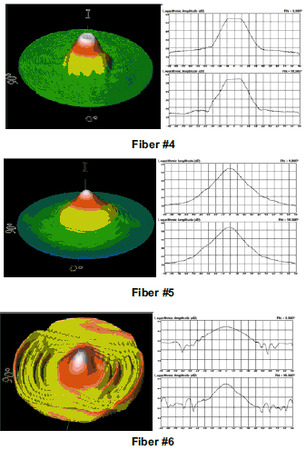
Photon recently conducted a study measuring commercially available tapered and lensed fibers to better understand the issues surrounding MFD measurements of these fibers. The results were generated using a Photon Model LD 8900HDR Far-Field Profiler with the fibers coupled to a stable, narrow-linewidth source operating at a nominal wavelength of 1550nm at an output power of 7 dBm. The full 3-D far-field profile and two orthogonal 1-D cross-sections are displayed below, as well as the average Mode Field Diameters determined from the Petermann II integral.
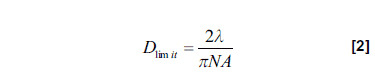
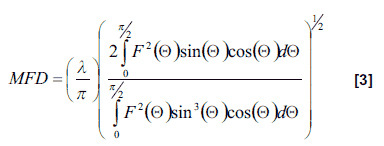
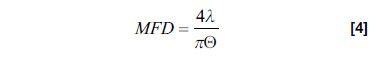

 Ultra-High Velocity
Ultra-High Velocity