Jeffrey L. Guttman, Ph.D., Director of Engineering, Ophir-Spiricon
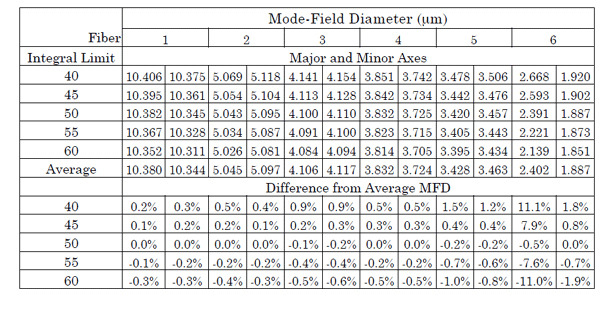
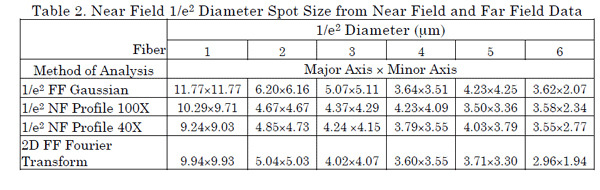
Lensed and Tapered specialty fibers are designed to optimize coupling between the fiber and various optical components such as edge-emitting laser diodes and AWGs. The light from these fibers forms a focus at some finite distance away from the fiber end. The MFD and corresponding spot size of these fibers is typically in the range of 5 microns or less. These small spot sizes and corresponding high divergence present challenges to near field and far field measurements. Typically the near-field measurements are limited by the optical performance, and the far-field measures must extend to very large angles. Results of measurements of 6 commercially available fibers are presented, including different type lensed/tapered fibers (4 axially symmetric and 1 elliptical) and a standard single-mode fiber for reference. Also, since the focused beams are in free space, there are some fundamental questions as to the applicability of the MFD, a measure originally formulated to describe the field distribution within a fiber.
The fibers were coupled to a stable narrow-linewidth diode laser source operating at a nominal wavelength of 1550 nm and output power of approximately 7dBm.
Far-field profiles were obtained using a 3D scanning goniometric radiometer, with optical dynamic range greater than 60 dB. This instrument provides NIST-traceable measures of MFD to the 0.5% level for single-mode fiber. The angular measurement range for each scan is ±90°, with sampling every 0.055°. By rotating the source about the scan plane, a full hemispherical measure of the far-field profile is obtained. The 3D profiles for each fiber in this study consist of 50 azimuthal scans at increments of 3.6° about the fiber axis.
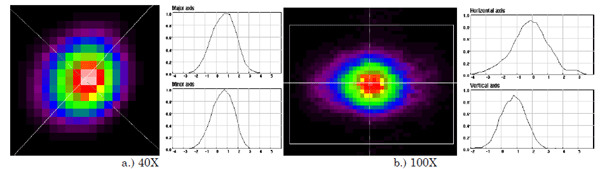
Near-field profile measurements were made using an IR Vidicon camera and 2 different magnifying objective lenses: a 100X NA 0.9 microscope objective intended for use in the visible and a 40X NA 0.48 aspheric lens designed for the IR. The point-spread function of this lens at 1550 nm is approximately 2.6 μm. The characteristics of the 100X lens at 1550nm are not known. The fibers were positioned using a high precision 3-axis translation stage. Absorbing glass filters were used for optical attenuation. The RS-170 camera video images were acquired using a framegrabber with 8-bit resolution, i.e., 256 levels. Measurement accuracy depends on the camera noise, sensor response uniformity, the digitization, the number of pixels in the image, and on the optical properties of the lens used. With adequate pixel count and lens quality, the signal noise and sensor response provide accuracy to the ±3% level. Accuracy is also strongly dependent on the lens position because of the short depth of focus of both the lens and the fibers being measured.
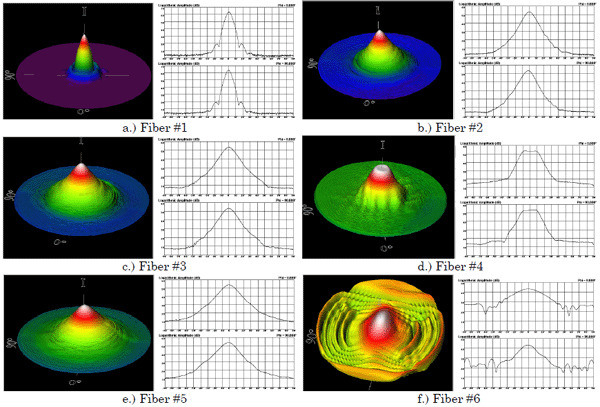
Complete hemispherical far-field profiles of the 6 fibers, (designated fibers # 1-6), and the corresponding 1D cross-sectional profiles through the principal axes of the distribution, are shown in figure 1. The background level of the measurements, seen in figure 1a for the profile of the standard single-mode fiber, is at the -60dB level relative to the peak. The profiles of the lensed/tapered fibers extend in all cases to ±90°. The profiles for fibers #1-5 have the appearance of a superposition of a main beam and a scatter background, probably due to surface modifications and defects introduced in the fabrication process. The angular extent of the main beam for these profiles ranges from approximately ±30° for the standard single-mode fiber to greater than ±70° for fiber #5. The profile for fiber #6, the elliptical fiber, consists of a main beam with a prominent diffraction structure. (Although not shown here, the scatter and diffraction structure extend to angles greater than ±90°, in the backward direction.)

 Ultra-High Velocity
Ultra-High Velocity