- Products
-
Solutions
- Industrial & Commercial
- Aerospace & Defense
- Scientific Research
- Life & Health Sciences
- Semiconductor
- Laser Measurement
- Directed Energy
- Laser Measurement
- Laser Skin Treatment (IPL)
- Laser Surgery
- Medical Imaging
- Disinfection with UV Light
- Infrared Optics
- Fever Detection
- Laser Optics
- PCB Via Drilling
- Semiconductor
-
Resources
- Literature & Software
- Laser Measurement
- Laser Beam Analysis
- IR Imaging Lenses
- Laser Optics
- LED Measurement
- Webinars
-
Support
- Service Returns & Calibration
- Returns & RMA Requests
- Calibration Service Centers
- Calibration Validity
- Calibration Portal
- Photonics Post Sale Product Support
- Policies & Certificates
- ISO Accreditation & Certificates
- Quality & Environmental Policy
- Volatility Statements
- Warranty Policy
- Terms of Sale
-
Blog
- Contact
-
- Sign In
- Orders
- en
-
Compare products
-
Product Comparison
Choose products to compare anywhere you see 'Add to Compare' or 'Compare' options displayed.
-
- Shopping cart items Shopping cart items
-
-
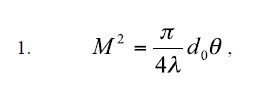
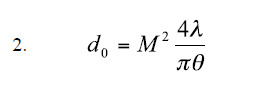
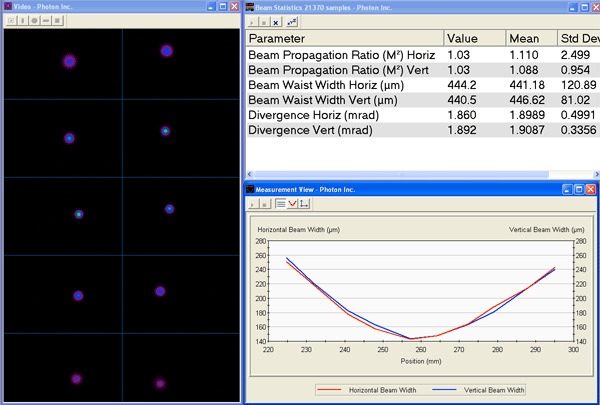
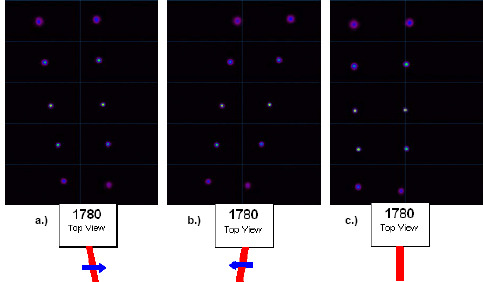
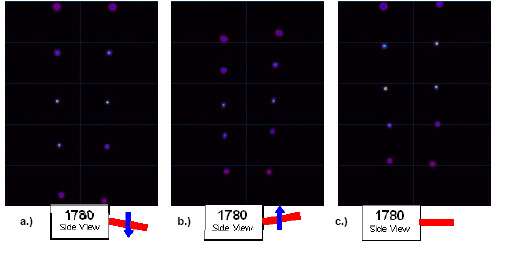
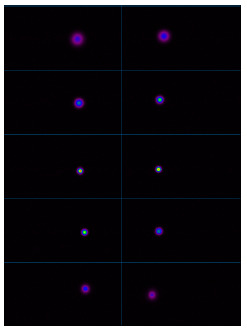
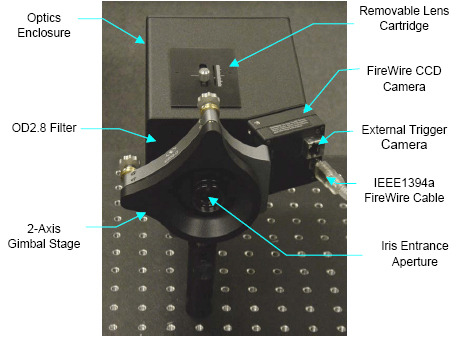
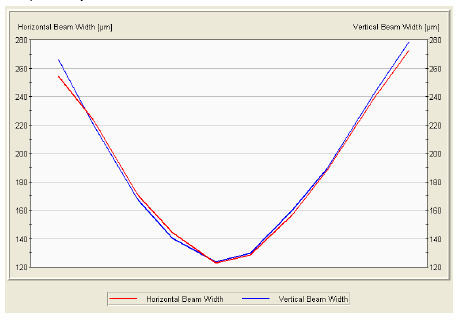
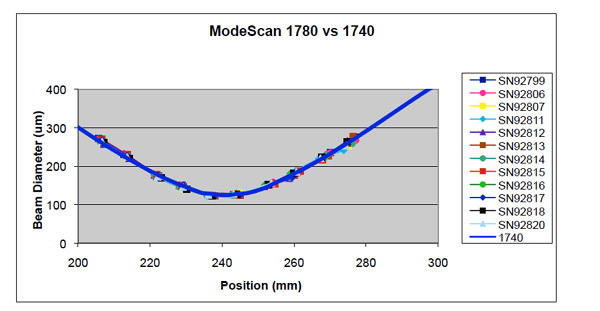
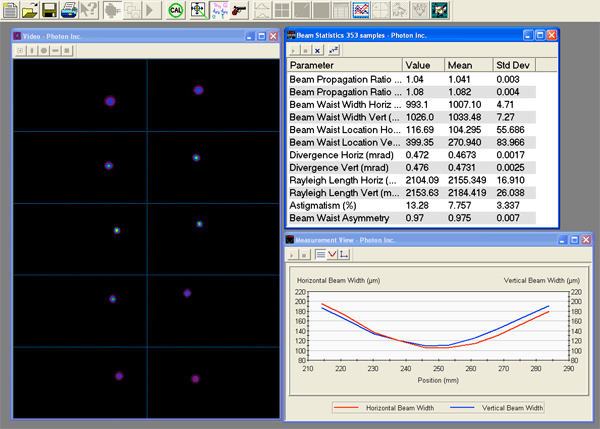
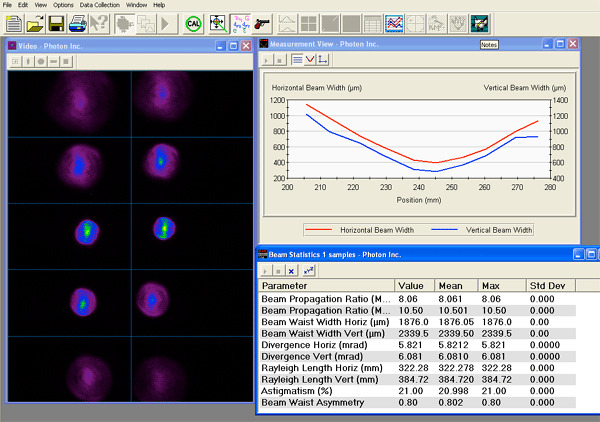
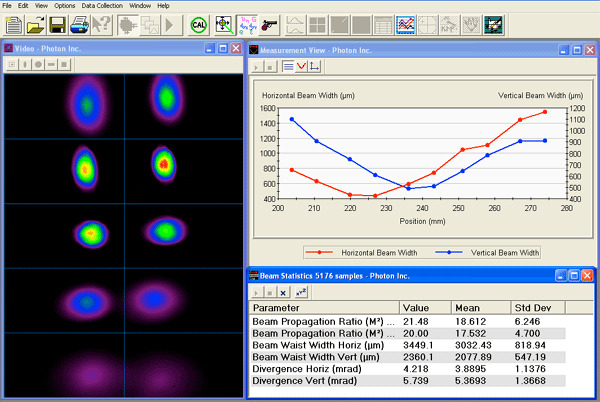
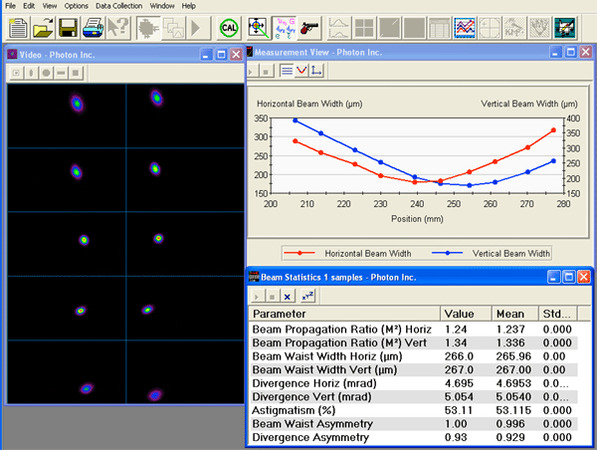
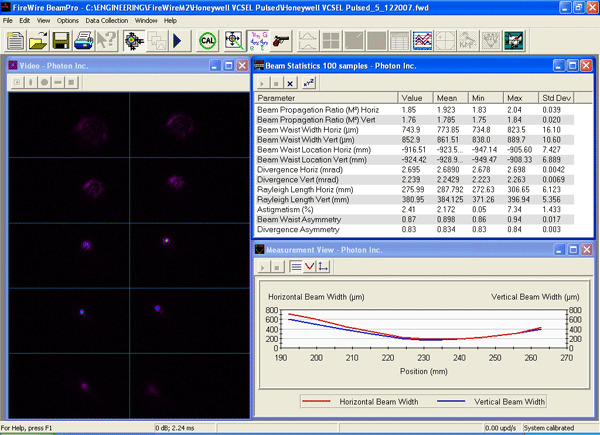
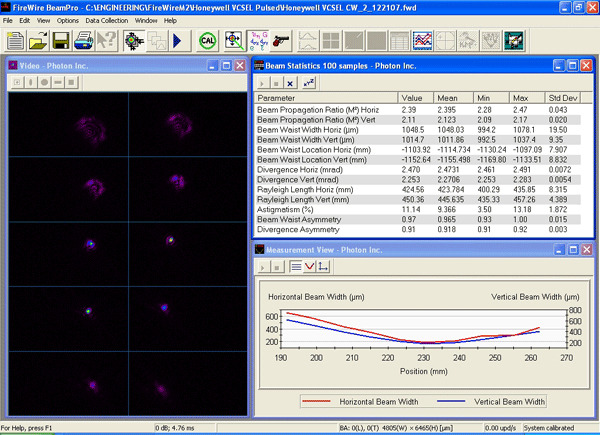
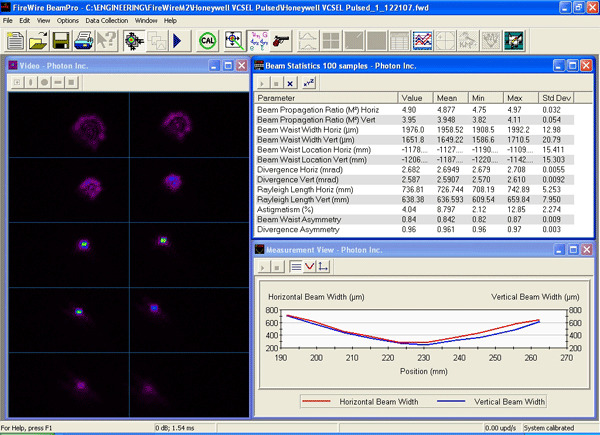

 Ultra-High Velocity
Ultra-High Velocity