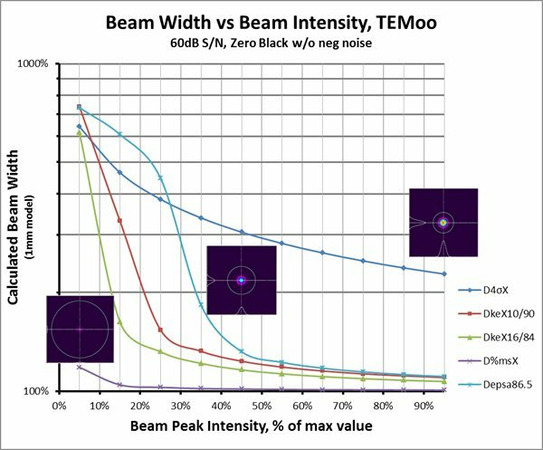
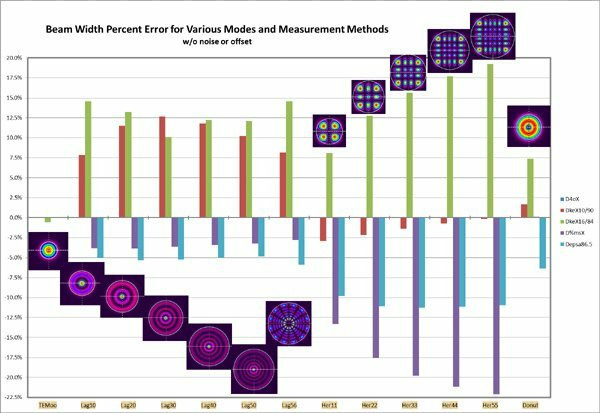
Note that for the TEM00 beam all of the methods yield highly accurate results, so accurate that they do not indicate on this type of bar chart graph. Only the ISO Knife Edge 16/84 method shows as reading slightly below 0%. For all higher modes this ISO method measures significantly high beam width errors. We provide this method in our BeamGage products only because it is ISO recommended. The Spiricon recommended 10/90 Knife Edge method also performs poorly for Laguerre modes, but is good for all Hermite and Donut modes. The Knife Edge methods are a good backup when operating in a high noise environment with Hermite modes as it is less effected by noise than is the D4σ calculation.
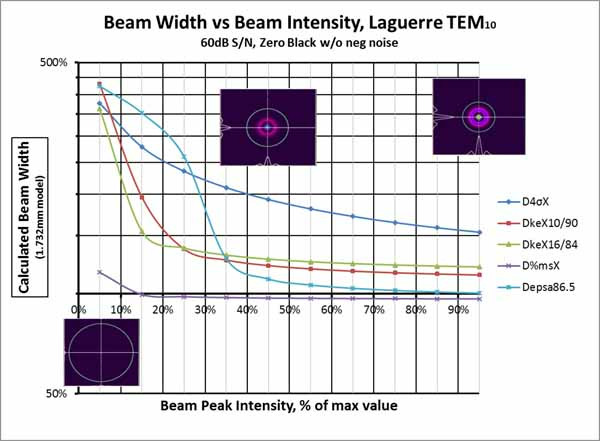
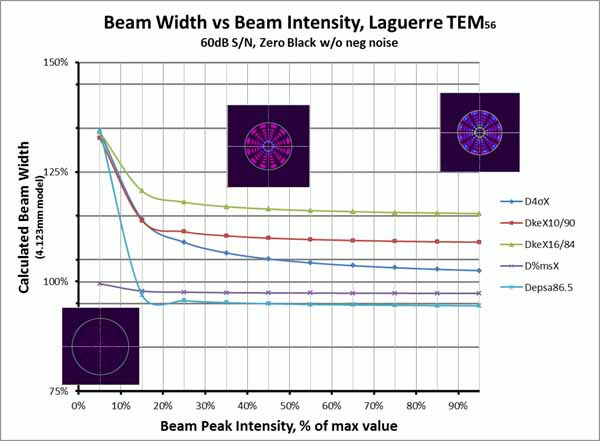
Observe that the Moving Slit method performs well with the Laguerre modes and very well with the Donut mode, but poorly with the Hermite modes. The moving slit method is a good backup when operating in a high noise environment for Laguerre modes.
The Encircled Power (Power in a Bucket) method is marginal with the Laguerre modes and poor with the Hermite and Donut modes.
Adding positive noise will, of course, shift the entire graph in the positive direction. A clip level could be employed to then shift the results back down. However, as is implied in the above graphs, a clip level that brings one mode under control may not be as good for other modes. Thus the dilemma of needing to know more about the beam than can be known in order to always employ just the correct clip level. And of course, for methods that under measure, even in the presence of noise, adding a clip level will only make things worse. Also most laser beams contain a mixture of higher modes, making the perfect clip level even more difficult to find.
Based on the above observations, what is needed is a method to cancel out the effects of the noise, and then apply the second moment D4σ method, as it will lead to the most fundamentally consistent beam width results. We will also retain the other methods to see if they too can be improved upon.
Most modern monochrome cameras come with a number of user configurable options, such as:
- Adjustable Gain
- Adjustable Black Level
- Electronic Shutter (Exposure) control
- Auto Gain
- Auto Black Level
- Auto Exposure control
- Region of Interest
- Auto Iris
- External Trigger Input
- Frame Sync Output
- Gamma
- Etc
None of the automatic features are useful for laser beam measurement. Gamma correction should also be turned off, i.e. set to one. External trigger is useful when capturing a pulsed laser. The top three items are important controls and must be setup correctly in order to achieve good operation. Gain should be set high enough to keep the camera operating in its linear response region, but not so high as to needlessly boost noise. Exposure control is set to prevent video saturation for CW lasers and to split out a single pulse when measuring a pulsed laser.
The key to noise cancelling lies with the Black Level control. In the first models, we assumed the camera had a perfectly adjusted black level. In the days of analog cameras this black level was referred to as the Pedestal. It typically contained positive noise but clipped off the negative noise. With a modern digital camera, the Black Level can be adjusted to raise the noise floor, or lowered to clip the noise to zero. Lowering it is essentially the same as adding a positive clip level to the input beam data. Raising it can bring the noise floor up. Raising it high enough can eliminate all zero counts. This raised noise floor will contain a temporal footprint of not only the camera noise, but also any inherent shading, along with any high and low offset pixels. By blocking the camera from light, and then averaging this signal, an accurate black level baseline can be computed for each pixel and then subtracted from the real time images obtained by the camera. The result is a new zero baseline that contains both positive and negative noise. In addition, the averaging process also computes the baseline to sub-pixel count precision. By retaining these fractional counts, the overall zero compensates for sub pixel quantization error. This error can be significant when millions of pixels are shifted up or down by a fraction of a count.
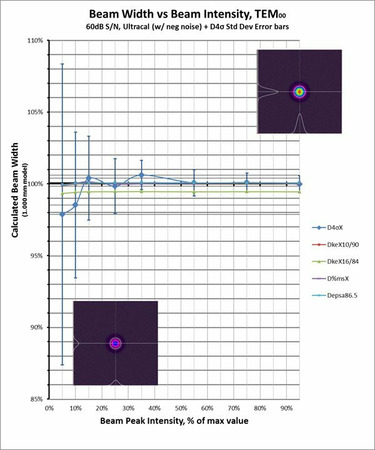
Figure 2-5 illustrates the computed beam widths for a TEM00 beam but with a properly corrected baseline that retains the negative noise. This is essentially graph 2-1 recomputed using Spiricon's Ultracal process. The actual errors will now become quite small (standard deviation <0.5% for most data points) except for the D4σ method. The noise in the outlying regions will seriously impact the second moment results. This is indicated by the standard deviation error bars plotted for the D4σ results.
Like all of the data, the D4σ data points are based on the averaged results of 16 frames. The second moment error bars indicate that the value calculated for any one frame is undergoing a wild ride both above and below the modeled beam width. Thus it is clear that to directly compute an accurate second moment beam width requires more assistance than just preserving the negative noise.
For all of the other computational methods, preserving the negative noise now yields an accurately computed beam width for a TEM00 beam. Except for the Knife Edge 16/84 method, all of the plots lie on top of each other at the 100% mark. The KE 16/84 method has a small 0.5% negative bias as indicated in the 2-4 graph.
Figure 2-3 hinted that as the beam filled more of the imager area, the beam width results became more accurate. In Part 3 we will investigate how proper use of an aperture to isolate the beam will give us the next step in finding an accurate second moment method. Then in the final part of this paper we will leave the world of models and look more closely at the real world of cameras and scanning slit technologies.

 Ultra-High Velocity
Ultra-High Velocity